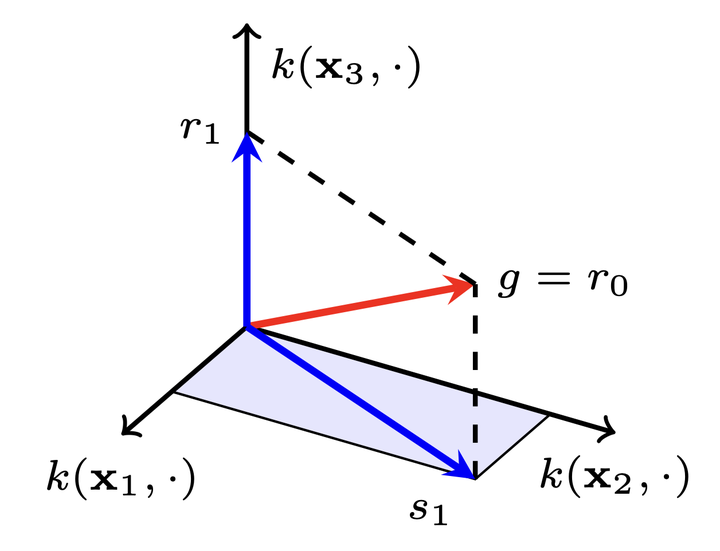
Illustration of alternating projection onto the subspace spanned by the kernel functions centered at the first two datapoints.Abstract
Gaussian process (GP) hyperparameter optimization requires repeatedly solving linear systems with n×n kernel matrices. To address the prohibitive O(n^3) time complexity, recent work has employed fast iterative numerical methods, like conjugate gradients (CG). However, as datasets increase in magnitude, the corresponding kernel matrices become increasingly ill-conditioned and still require O(n^2) space without partitioning. Thus, while CG increases the size of datasets GPs can be trained on, modern datasets reach scales beyond its applicability. In this work, we propose an iterative method which only accesses subblocks of the kernel matrix, effectively enabling mini-batching. Our algorithm, based on alternating projection, has O(n) per-iteration time and space complexity, solving many of the practical challenges of scaling GPs to very large datasets. Theoretically, we prove our method enjoys linear convergence and empirically we demonstrate its robustness to ill-conditioning. On large-scale benchmark datasets up to four million datapoints our approach accelerates training by a factor of 2× to 27× compared to CG.